What's reinforcement learning?

End-to-end learning for Sequential Decision Making

What does end-to-end mean for

Sequential Decision Making?

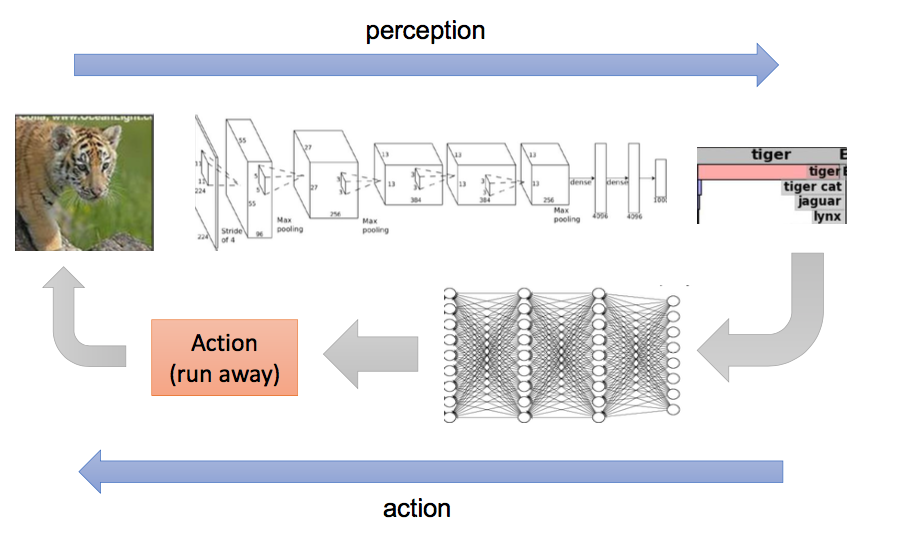
More formally!

Comparison with deep learning framework

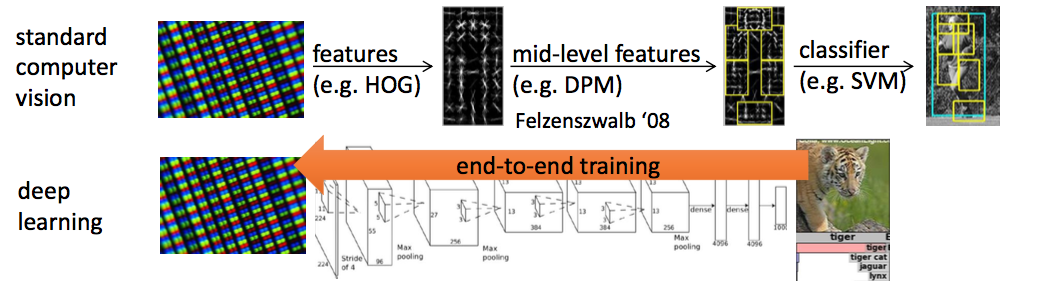
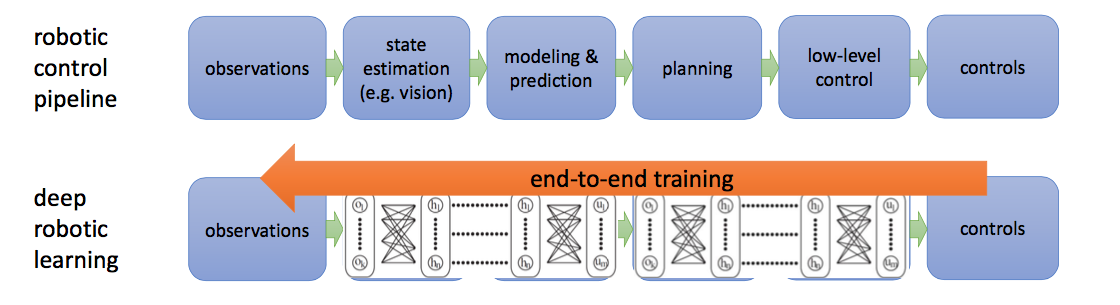
Short Summary (DRL)

• RL originates from the need for sequential decision making process
• DL is analogous to one state of the "sequence"
• DL allows RL to solve complex problems end-to-end

Mathematical Definitions

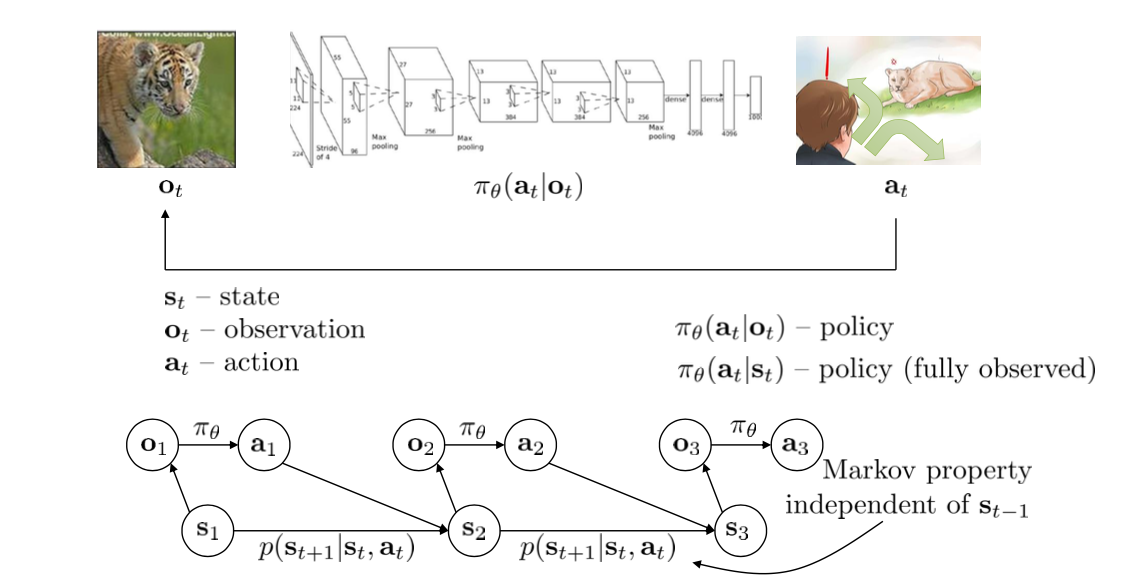
The goal of reinforcement learning

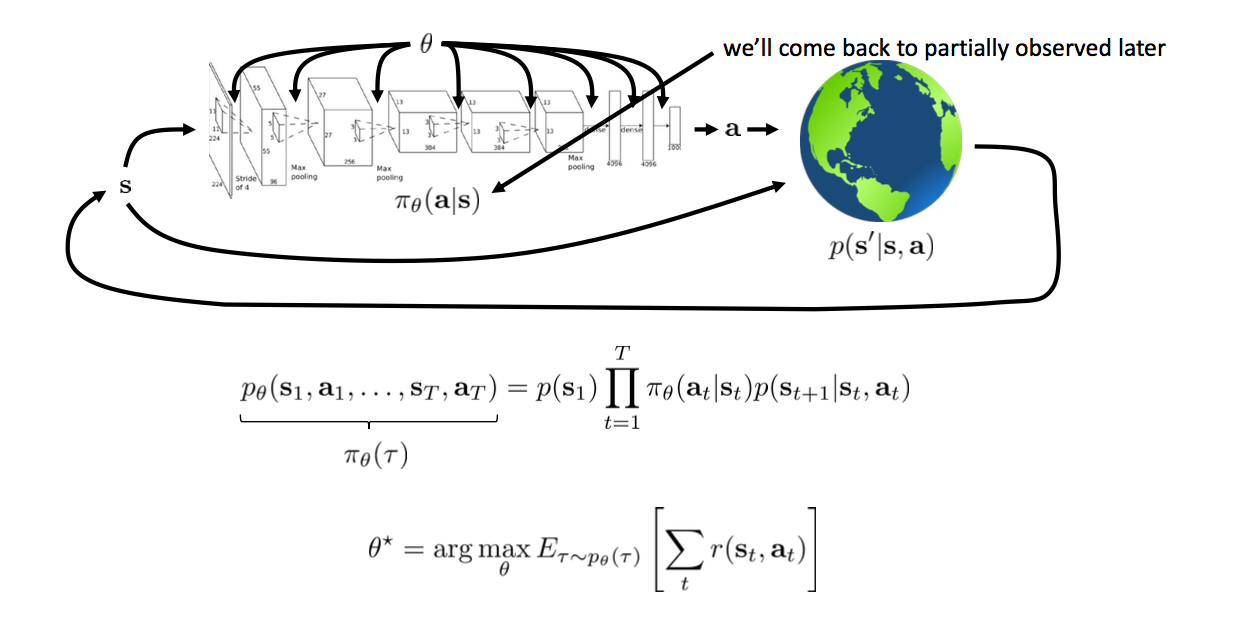
Toy Examples

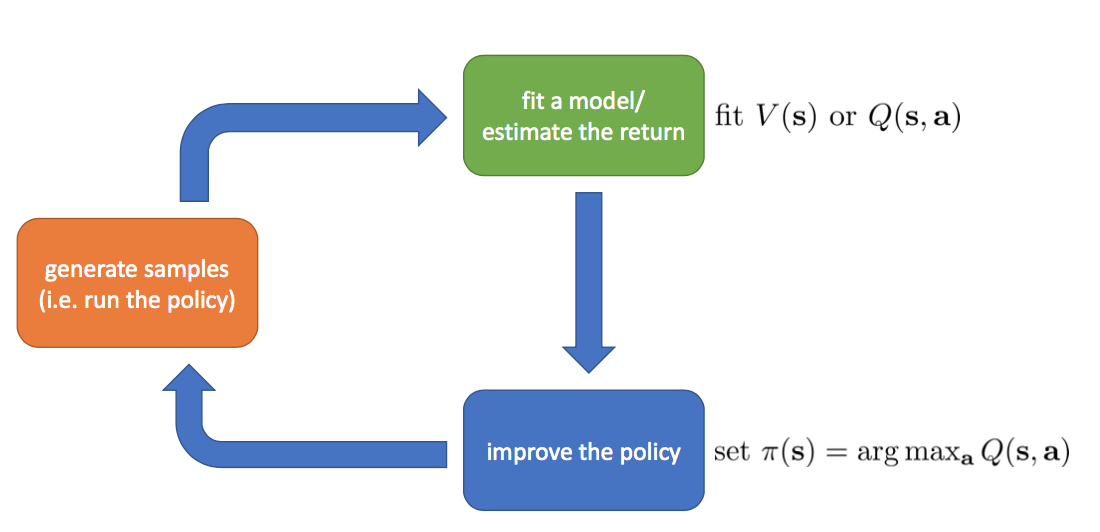
1. Value-based: Indirectly optimize policy via estimation of value function
2. Policy gradients: Directly optimize policy by calulating gradient of policy
3. Actor-critic: Combination of above two

Value Iteration

$V^{*}_{k}(s)\leftarrow max_{a}\sum_{s'}P(s'|s,a)(R(s,a,s')+\gamma V^{*}_{k-1}(s))$

$\pi_{k}^{*}(s)\leftarrow argmax_{a}V^{*}_{k}(s)$

Policy Gradients

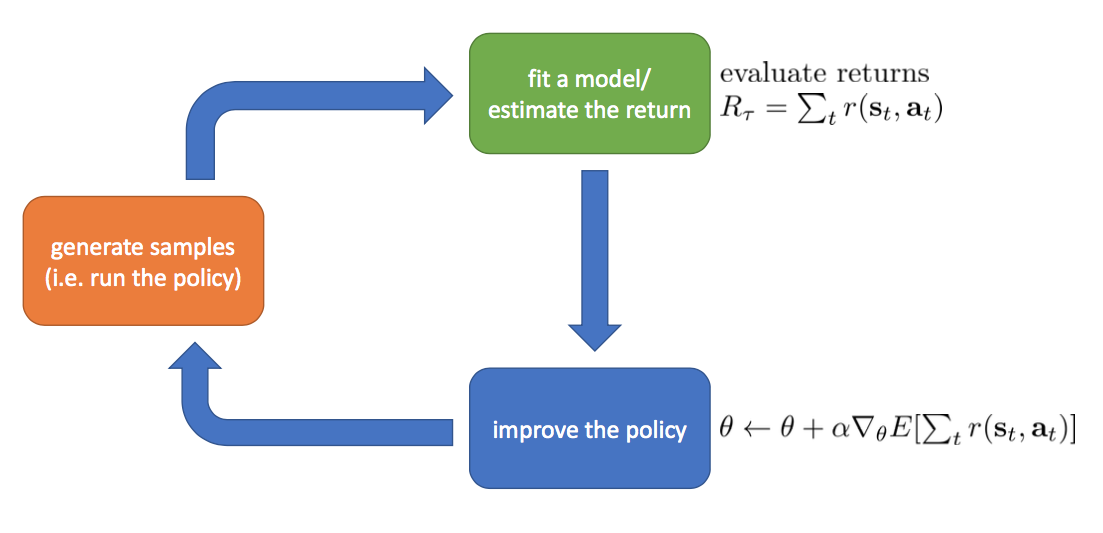
Policy Gradients

$ U( \theta )=E[ \sum_{t=0}^{H}R(s_{t},u_{t});\pi_{\theta}]=\sum_{ \tau }P(\tau;\theta)R(\tau)$

$\bigtriangledown _{\theta}U( \theta )= \bigtriangledown _{\theta}\sum_{ \tau }P(\tau;\theta)R(\tau)=\sum_{ \tau }\bigtriangledown _{\theta}P(\tau;\theta)R(\tau) $ $ =\sum_{ \tau }\frac{P(\tau;\theta) }{P(\tau;\theta) } \bigtriangledown _{\theta}P(\tau;\theta)R(\tau) $ $=\sum_{ \tau }P(\tau;\theta)\frac{\bigtriangledown _{\theta}P(\tau;\theta) }{P(\tau;\theta) }R(\tau) $ $ =\sum_{ \tau }P(\tau;\theta)\bigtriangledown _{\theta}logP(\tau;\theta)R(\tau) $ $= \frac{1}{m} \sum_{i=1}^{m}\bigtriangledown _{\theta}logP(\tau^{(i)};\theta)R(\tau^{(i)})$

Policy Gradients

# Given:
# actions - (N*T) x Da tensor of actions
# states - (N*T) x Ds tensor of states
# q_values – (N*T) x 1 tensor of estimated state-action values
# Build the graph:
logits = policy.predictions(states) # This should return (N*T) x Da tensor of action logits 
negative_likelihoods = tf.nn.softmax_cross_entropy_with_logits(labels=actions, logits=logits) 
weighted_negative_likelihoods = tf.multiply(negative_likelihoods, rewards)
loss = tf.reduce_mean(weighted_negative_likelihoods)
gradients = loss.gradients(loss, variables)
						

$\frac{1}{m}\sum_{i=1}^{m}\sum_{t=1}^{T}\bigtriangledown _{\theta}log(\pi_{a_{i,t}}|s_{i,t};\theta)\widehat{R_{i,t}}$

Actor Critic

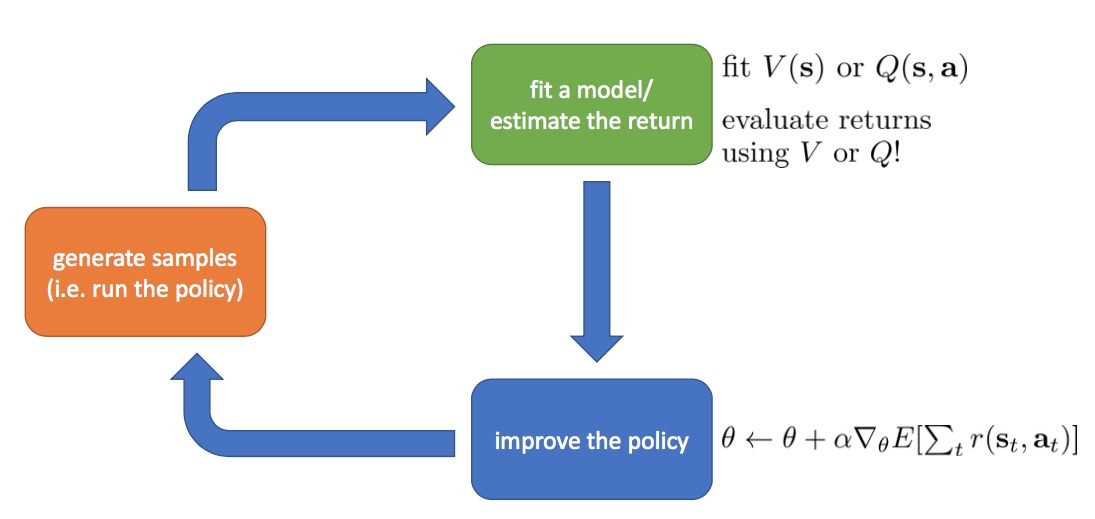
What have we come so far?

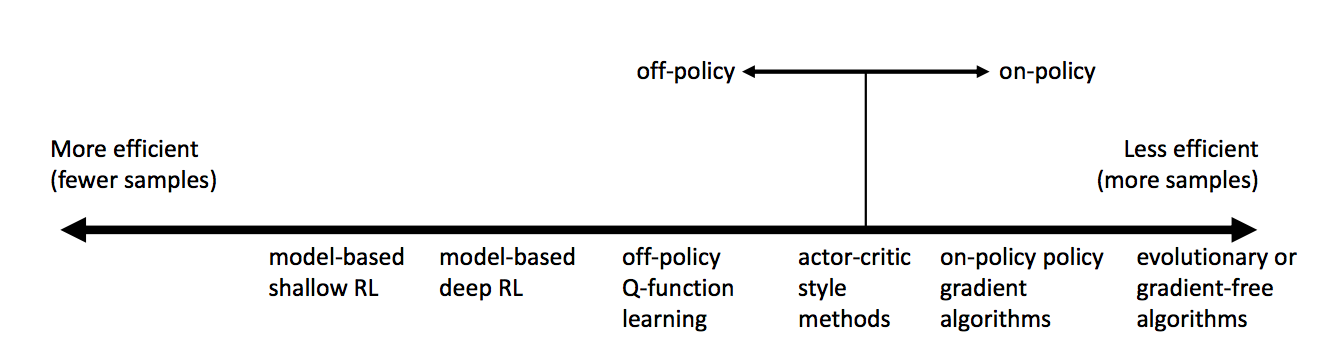
Getting Serious

Look Before You Leap: Bridging Model-Free and Model-Based Reinforcement Learning for Planned-Ahead Vision-and-Language Navigation

Task description

Components

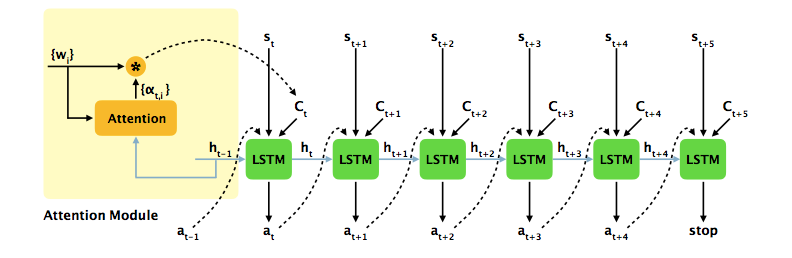
							# Recurrent policy model
							e(t,i)=tf.matmul(h(t-1).transpose(),w(i))
							a(t,i)=tf.exp(e(t,i))/tf.reduce_sum(tf.exp(e(t,k)), axis=1)
							c(t)=tf.reduce_sum(a(t,i)*w(i))
							h(t)=LSTM(h(t-1),[c(t),s(t),a(t-1)])

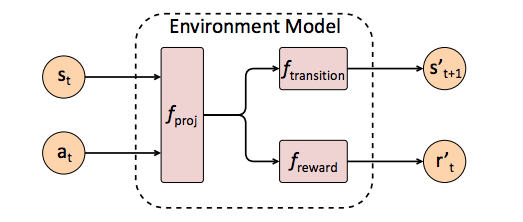
							# Environment model
							s(t+1)=fransition(fproj(st,at))
							r(t+1)=freward(fproj(st,at))
						

Model Pipeline

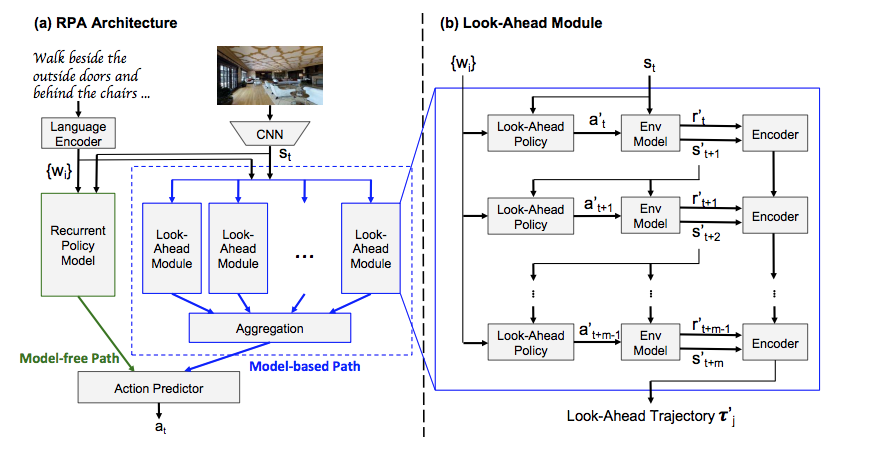
Model Learning

• Pretrain environment model with immitation
• Freeze environment model and train policy model

							# Immitation learning
							Train environment model with Randomized teacher poclicy;
							Pick demonstration policy with P=0.95;
							Pick Bernouli Meta policy with P=0.05;

							l_transition=E[s'(t+1)-s(t+1)]
							l_reward=E[r'(t+1)-r(t+1)]

							# Policy learning
							r(st,at)=distance(s(t))-distance(s(t+1))
							R(st,at)=discounted total sum of r
							Perform REINFORCE algorithm on R
						

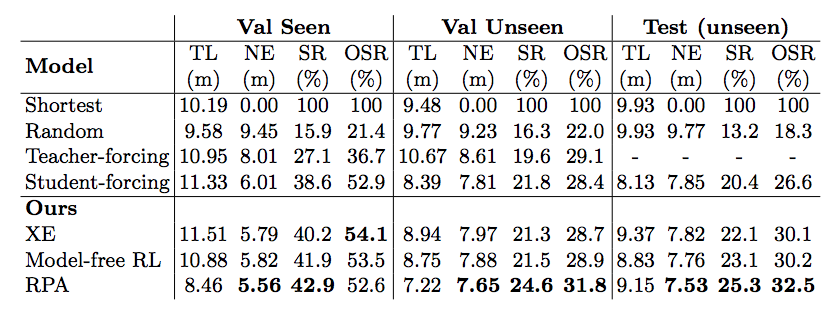
Result

My current work

• Modularize unified RL interface for benchmarking important ideas
• Parallelize RL codebase for faster iteration
• Try new ideas on indoor navigation

Benchmarking Efforts

• Verify code correctness
• Building blocks

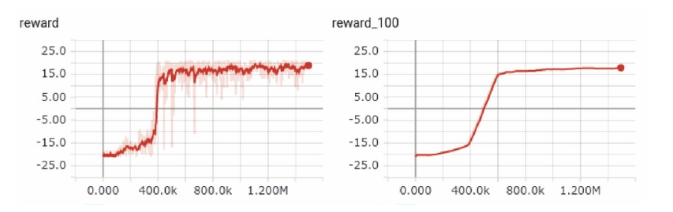
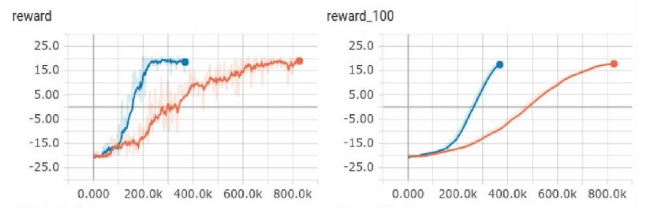
Vanilla DQN & 2-step unrolling DQN;

Advanced DQNs

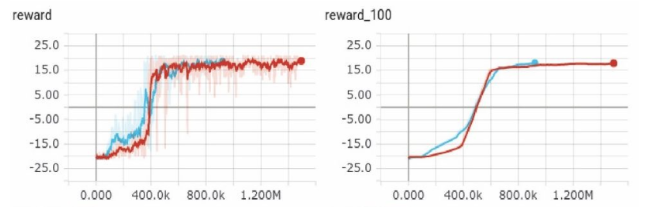
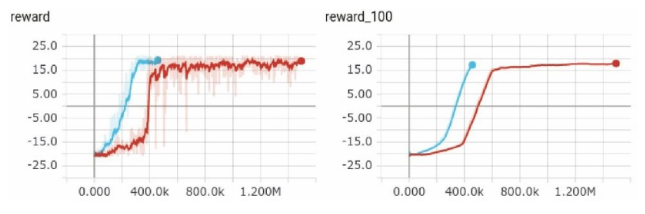
Double DQN & duelling DQN;

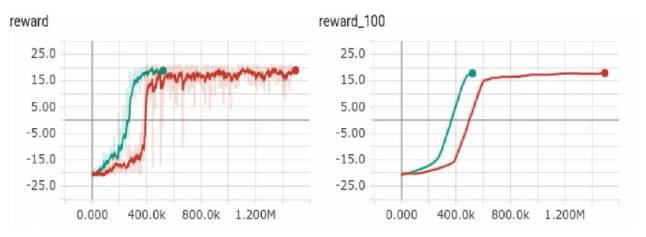
Prioritized Experience Replay;

Policy-based methods and its variance

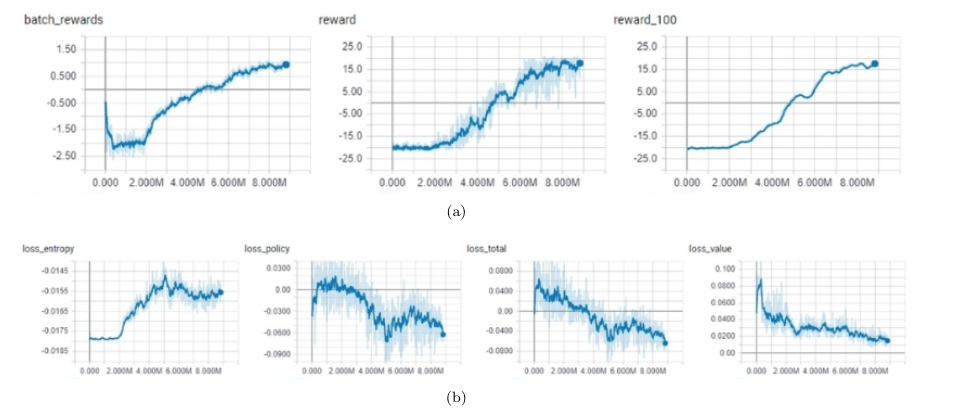
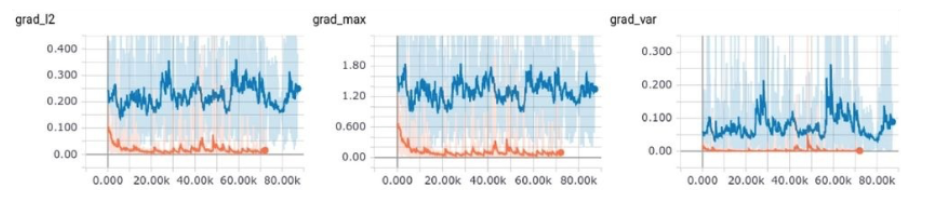
Parallelization

• Data Parallelism
• Gradient Parallelism

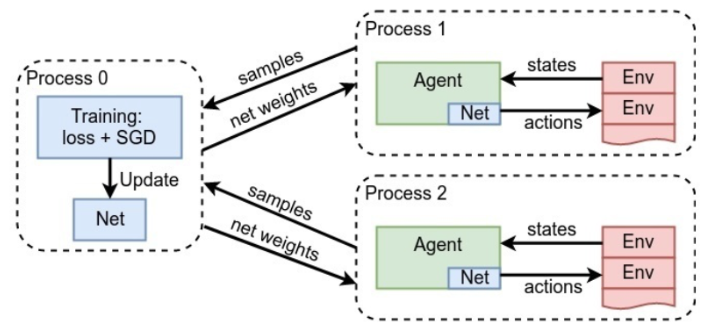
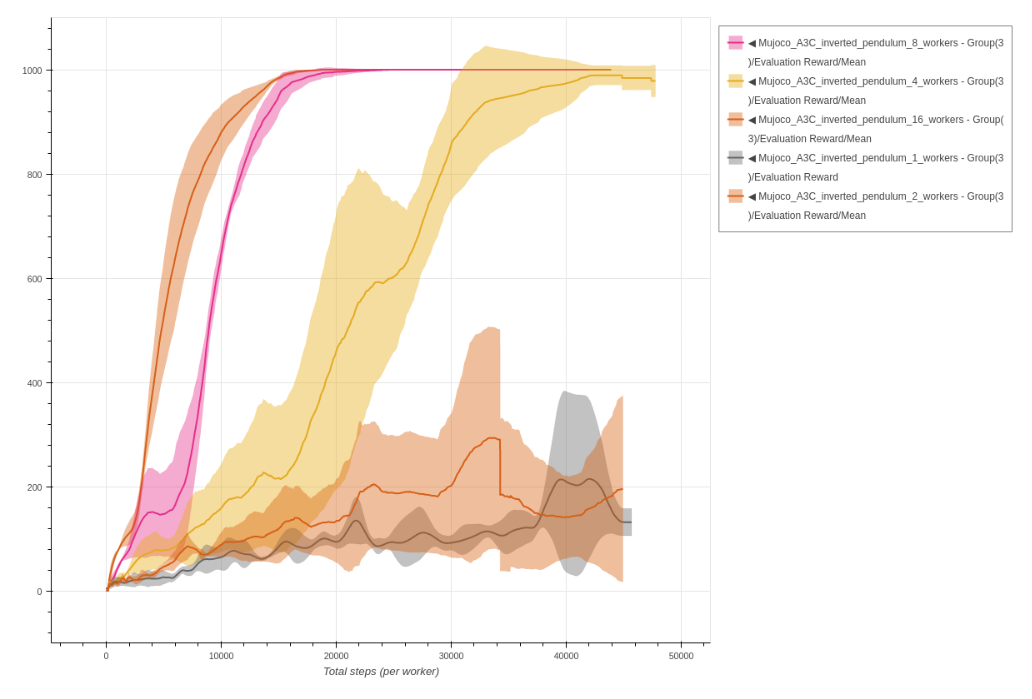
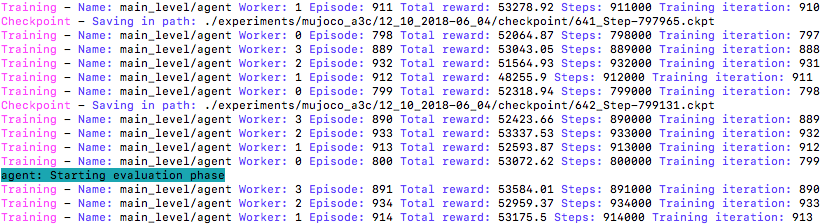
Develop new ideas

Examples

• Improve sample efficiency
• Develop explorative agents
• Consider tasks with sparse rewards
• Multi-agent communication